Числовой инструментарий, часть III
Автор: (C) Кристоф Шпиль [Christoph
Spiel]
Перевод: (C) С. Скороходов
В первой и второй частях этой мини-серии о математических инструменах от GNU/Linux речь шла о таких довольно "сухих" предметах, как манипуляции матрицами и циклы for. Эта часть добавляет на экран многоцветье, т.к. мы переходим к описанию графических возможностей GNU/Octave, Scilab и Tela. Вынуждено отойдем от принятого в предыдущих частях стиля изложения: описывать все три программы вместе. Дело в том, что "графические движки", стоящие за каждой программой, рознятся столь существенно, что их работу нельзя описать "одним блоком", отделавшись несколькими замечаниями по поводу различий.
Тем не менее, статья начинается с введения, имеющего равное отношение сразу ко всем прогрммам. Для максимизации удобства читателя, все три программы будут решать три одинаковые проблемы из реальной жизни, что облегчит сравнение несмотря на имеющиеся различия в реализации. В последующих разделах Octave, Scilab и Tela придется справляться с предложенными задачами.
Введение
- Только дискретные данные!
-
Все три приложения предназначены для работы исключительно с векторами и матрицами и их графические подсистемы понимают только такие данные. Вот так! С точки зрения пользователя это означает, что график функции вроде этой
{ sin(x)/x for x <> 0 y := f(x) = { { 1 for x == 0не может быть нарисован на основании приведенного выражения. Вместо этого, функция должна быть представлена в ввиде пар дискретных значений (x(i), y(i)). Для получения значений f(x) мы берем значения x, соответствующие интересующим нас местам f(x), и вычисляем для них значение f. Любой, кто прочел передыдущие части, немедленно поймет, что здесь применяются векторные операции.
### GNU/Octave code
function y = f(x) if x == 0.0 y = 1.0; else y = sin(x) ./ x; endif endfunctionx = linspace(0.0, 4*pi, 50); y = f(x);linspace(start, end, n) возвращает вектор, n элементов которого равномерно распределены между start и end. Векторы x и y могут быть переданы соответствующим функциям отрисовки графиков.
Если данные уже в векторной форме, то "изобразить" их можно немедленно.
- Глобальная сложность
-
Как мы фактически рисуем график? Этот вопрос приводит к фундаментальной проблеме, с которой при графическом отображении данных сталкиваются все приложения: что выгодней -- один вызов "навороченной" функции или несколько вызовов функций "попроще"?! Для начала рассмотрим сложность вызовов, с которой пользователь сталкивается при решении системы линейных уравнений
x = a \ b # Octave, Scilab
или
x = linsolve(a, b) // Tela
Даже если мы сильно постараемся усложнить вызовы (сохраняя их полезность), то придем к следующему
x = linsolve(a, b, "CompletePivoting", "DoIterativeRefinement")
Таким образом, два дополнительных параметра -- стратегия обращения [pivoting] и последовательные приближения [iterative refinement] -- и пользователь полностью управляет поведением linsolve(). Все остальные "решения" вполне может взять на себя программа: например то, какой алгоритм использовать в случае, если матрица a имеет специальную форму.
Сравните эту задачу с построением двухмерного графика:
x = [2.25, 2.27, 2.42, ...] y = [0.363, 0.360, 0.337, ...]
Какие тут могут быть варианты?
- Изобразить данные в виде изолированных точек или соединить точки прямыми линиями.
- Какой символ использовать для изображения данных? Точку, звезду, кружок или звездочку? Какого цвета?
- Каким должен быть вид соединяющей значения линии? Непрерывная, штриховая, пунктирная или штрих-пунктирная? Какими должны быть толщина и цвет линии?
- Нужно ли масштабировать график для того, чтобы он поместился в окно вывода?
- Рисовать ли координатные оси? Должна ли ось x или y быть логарифмической? Обе оси логарифмические?
- Нужны ли делать на осях надписи и рисовать деления?
- ...
Можно придумать еще... Смысл в том, что создание графиков не может быть столь же простым, как, например, решение линейных уравнений -- не потому, что программы написаны скверно, а оттого, что сложнее сама суть действий пользователя. Так что не стоит удивляться тому, что в Octave, Scilab или Tela понадобится 20 и более строк кода для создания диаграммы типографского качества.
Задачи
Для того, чтобы соревнование программ было интересным, я составил задачи, не слишком отличающихся от тех, которые ставит Жизнь(tm). Каждой из трех программ придется справится с построением графиков трех разных видов:
- Двумерный график
дискретных данных
Отображение трех наборов данных (l1.ascii, l2.ascii, l3.ascii) на одной странице. Наборы содержат различное число значений.
Данные представлены в виде двух колонок, первая содержит значение X, вторая -- Y:
0.2808 3.419E-07 0.3711 3.459E-07 0.4882 3.488E-07 ...
График должен иметь название, имена осей и легенду. Диапазон значений x и y указывается пользователем.
- Трехмерный график
функции
Отображает функцию Rosenbrock'а (в двух измерениях)f(u, v) = 100*(v - u^2)^2 + (1 - u)^2
как трехмерную поверхность в диапазонах значений параметров -3 <= u <= 3 и -2 <= v <= 4.
Добавить к графику аннотацию и название осей.
- Контурный график
функции
Изобразить функциюg(u, v) = exp(u) * (4*u^2 + 2*v^2 + 4*u*v + 2*v + 1)
в виде контуров, а именно f(u, v) = z для данного z в диапазоне параметров -4.5 <= u <= -0.5 и -1 <= v <= 3.
Изолинии определяются пользовательской "весовой" функцией.
( z - z_0 ) 3 z_iso = (z_1 - z_0) * ( --------- ) + z_0 ( z_1 - z_0 )где z_0 и z_1 -- минимальное и максимальное значение g(u, v) в пределах значения графика.
На графике, как всегда, должны быть заголовок и обозначение осей координат.
Все графики должны быть выведены на два устройства,
- терминал X11 и
- принтер Postscript.
Octave
Вы знакомы с Gnuplot? Тогда использование создание графиков в GNU/Octave
Вы освоите играючи. Все, что понадобится -- добавить "g"
перед командой Gnuplot -- и Вы получаете эквивалентную команду Octave.
А-а, Вы еще не пробовали работать с Gnuplot? Тогда я буду Вашим проводником.
Тем не менее, руководство по Gnuplot (электронное или выпущенное на
умерщвленной древесине) будет полезным.
Octave: двухмерный график дискретных данных
Для облегчения обсуждения я разбил код на блоки. В каждом блоке сгруппированы связанные по смыслу команды, а сам блок помечен цифрой в квадратных скобках для того, чтобы в дальнейшем было легче на него ссылаться.
### [1] Считать данные из set_i в матрицу размерности N_i-times-2
set1 = load("l1.ascii");
set2 = load("l2.ascii");
set3 = load("l3.ascii");
### [2] Переинициализирвать Gnuplot
graw("reset;");
clearplot;
### [3] Определить оформление графика
### во избежания проблем с кириллицей при выполнении примеров
### английские надписи не переводятся, а поясняются кое-где в комментариях,
### если эти комментарии будут мешать -- уберите их
### попытка вывода кириллических подписей
### оставляется в качестве самостоятельного упражнения читателю:)
### само собой, типа примечание переводчика:)
gset title "Comparison of sets L1, L2, and L3";
### Сравнение наборов данных L1, L2 и L3
gset xlabel "Temperature / K";
### Температура, Кельвины
gset ylabel "Voltage / V";
### Напряжение, Вольты
gset key top left;
gset xrange [0 : 100];
gset yrange [8e-8 : 2e-6];
### [4] Отрисовка графика
hold on;
### Набор L1
gplot set1 title "Set L1" with points;
### Набор L2
gplot set2 title "Set L2" with points;
### Набор L3
gplot set3 title "Set L3" with points;
hold off;
### [5] Переключаемся на вывод графика в файл PostScript
gset terminal push;
gset terminal postscript;
gset output "oct1.eps";
replot;
gset terminal pop;
gset output;
![[Графический файл: Окно Gnuplot, открытое из графическими командами Octave
и показывающее три набора данных. Точки, изображающие данные показаны синими,
зелеными и красными маркерами. Маркеры имеют разную форму. На осях имеются пояснения,
определенные в командах gset.]](misc/spiel/oct10000.png)
Вывод на Postscript из блока [5] создал пригодный
для печати файл eps.
Блок [1] должен быть понятен на основе материала предыдущих статей. Взаимодействие с Gnuplot в первый раз происходит в блоке [2], где Gnuplot приводится в заранее известное состояние и X11-окно очищается для отрисовки графика. Заранее известное состояние полезно при экспериментировании с настройками Gnuplot. В нашем случае переинициализация не требуется, но и вреда от нее никакого.
Смысл блока [3] из команд gset очевиден, за исключением
gset key top left
что означает "поместить легенду (или "ключи" [key]
внутрь области отрисовки графика, в ее северо-западный угол".
Аргументы xrange и yrange (со специальным
синтаксисом задания интервалов) устанавливают ширину и высоту графика
в соответсвии с диапазонами значений отображаемых данных.
Теперь данные могут быть изображены на графике [4]. Поскольку размеры
наборов данных различны, их нельзя объединить в одной матрице. Следовательно,
каждый набор приходится отображать самостоятельно, а Gnuplot должен
быть проинформирован -- командой hold on -- о том, что
от него требуется накапливать команды gplot до тех пор,
пока отрисовка последней кривой не завершится и не будет вызвана команда
hold off. Вызовы gplot, понятно, содержат
указание на матрицу с данными
gplot set1
Название кривых, которое должно появится в легенде, также передается
в вызове gplot.
Блок [5] типичен для "механизма" работы Gnuplot. Для
выполнения каждой команды отрисовки он использует терминал:
параметр terminal и файл вывода: параметр output
(помните, что в UN*X все является файлом, в частности консоль). Когда
Gnuplot выполняется в среде X, тип терминала по умолчанию -- X11,
а файл вывода -- графическое окно. И terminal, и output
могут быть изменены независимо командами gset. Таким
образом, для получения тех же самых графиков в другом формате мы изменяем
текущий терминал на Postscript, а в качестве файла вывода задаем подходящее
имя дискового файла. Функция replot проигрывает все команды
рисования заново, так что нам не надо вводить их еще раз. После этого
все установки терминала и файла вывода отменяются, что не является
обязательным, но полезно в тех случаях, когда пользователь собирается
поиграться с дополнительными вызовами gset, проверяя
их влияние на вид получаемого графика.
Octave: Трехмерный график функции
### [1] Определение функции
function z = f(u, v)
## ограниченная [truncated] функция Rosenbrock'а
z = 100.0*(v - u.^2).^2 + (1.0 - u).^2;
zv = z(:);
zv(find(zv > 100.0)) = 100.0;
z = reshape(zv, size(z));
endfunction
### [2] Простая функция f()
x = linspace(-3, 3, 40);
y = linspace(-2, 4, 40);
[xx, yy] = meshgrid(x, y);
z_splot = splice_mat(xx, yy, f(xx, yy));
### [3] Переинициализация Gnuplot
graw("reset;");
clearplot;
### [4] Определим на графике украшения и пояснения
gset data style line;
gset title "Rosenbrock Function";
gset xlabel "u";
gset ylabel "v";
gset view 30, 160;
gset hidden;
gset nokey
gset parametric;
### [5] Отрисуем график
gsplot z_splot;
### [6] Переключимся на вывод в файл PostScript
gset terminal push;
gset terminal postscript;
gset output "oct2.eps";
replot;
gset terminal pop;
gset output;
gset noparametric;
system("gzip --best --force oct2.eps");
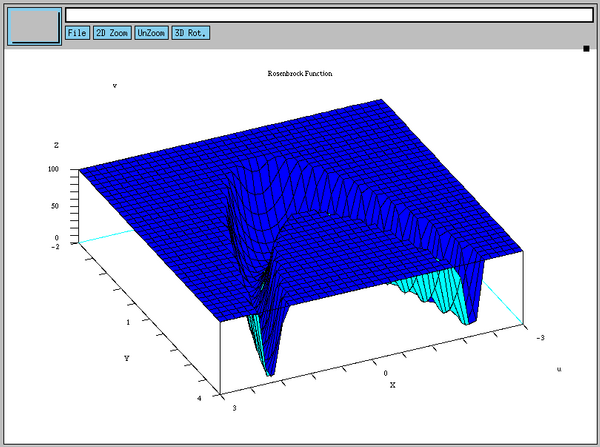
![[Рисунок: Окно Gnuplot с красной трехмерной сеткой, 'деформированной'
в соответствии с функцией f(u, v). График в целом похож на бумеранг...]](misc/spiel/oct20000.png)
Имеется и версия для печати (eps.gz).
Блок [1], как всегда, несложен для понимания (после прочтения 1-ой
и 2-ой частей этой мини-серии) и содержит исключительно известные
функции. В противоположность ему, блок [2] вводит в обиход парочку
новых. С помощью нашего друга linspace() мы легко создаем
два вектора, задающих точки для вычисления функции f(u, v):
из векторов x и y создается "решетка"
[grid], после чего в матрицах xx и yy каждая пара
элементов (xx(i, j), yy(i, j)), 1 <= i,j <= 40
задает точку (решетки), в которой будте вычисляться функция z = f(u,
v). Матрица всех значений z на точках решетки определяется,
как zz = f(xx, yy). Но мы еще не закончили, т.к. Octave
требуется передать функции gsplot (служит для построения
трехмерных графиков) матрицу, отформатированную особым образом.
Пользовательская функция splice_mat() делает как раз то, что нужно: составляет из описывающих решетку xx и yy и значений z матрицу z_plot. Эта матрица уже может быть передана gsplot без хлопот:) (исходя из предположения, что Gnuplot находится в параметрическом режиме [parametric mode]. (А мы, конечно, будем именно в параметрическом режиме, поскольку для подобных задач только параметрический режим и годится (а я не хочу добавлять еще уровень вложенности скобок (ну правда!))))
Блок [4] представляет из себя набор вызовов gset
и выглядит достаточно знакомым. Добавлено лишь несколько новых настроек
- gset data style line
Соединить соседние точки "сетки" [mesh] линиями (по умолчанию -- красного цвета). - gset view
x_angle, z_angle
Повернуть изображение на угол x_angle градусов отностительно оси x, а затем на z_angle градусов относительно оси z. - gset hidden
Подавление вывода невидимых линий сетки. Задняя сторона сетки будет отрисована иначе (зеленым цветом в окне X11и пунктирной черной линией на Postscript-терминале). - gset nokey
Не выводить легенду. - gset parametric
Посмотрите в документации по GNU/Octave (командаhelp -i gsplotв Octave илиinfo octave --node='Three-Dimensional Plotting'из шелла).
После такой тщательной подготовки команда блока [5] gsplot
z_splot, осуществляющая собственно графический вывод, выглядит
тривиальной.
Блок [6] отрисовки в Postscript похож на сходный блок [5] из секции Octave: двухмерный график дискретных данных. Единственно, что еще делает блок [6] -- сжатие eps-файла с помощью gzip. Вообще, вызов system("shell-commands") выполняет команды shell-commands в дочернем шелле. Совершенно очевидно, что это очень полезно для взаимодействия с такими внешними приложениями, как gzip(1).
Octave: Контурный график функции
### [1] Определение функций
function z = g(u, v)
z = exp(u) .* (4.0*u.^2 + 2.0*v.^2 + 4.0*u.*v + 2.0*v + 1.0);
endfunction
### [2] Определение весовых функций для расстояния между изолиниями
function y = pow_weight(x, n)
## Отображаем интервал X в себя, "взвешивая" возведением в степень N
d = max(x) - min(x);
y = d*((x - min(x))/d).^n + min(x);
endfunction
### [3] Используемая функция g()
x = linspace(-4.5, -0.5, 40);
y = linspace(-1.0, 3.0, 40);
[xx, yy] = meshgrid(x, y);
zz = g(xx, yy);
z_splot = splice_mat(xx, yy, zz);
### [4] Вычисление расстояние между изолиниями
iso_levels = pow_weight(linspace(min(min(zz))*1.01, ...
max(max(zz))*0.99, 12), 3.0);
il_str = sprintf("%f,", iso_levels);
il_str = il_str(1 : length(il_str)-1); # удаляем "," на конце
### [5] Переинициализация Gnuplot
graw("reset;");
clearplot;
### [6] Определение оформления и пояснений
gset data style line;
gset title "Contour Plot of g(u, v)";
### "Контурный график g(u, v)"
gset xlabel "u";
gset ylabel "v";
gset contour base;
gset nosurface;
gset view 0, 0;
eval(sprintf("gset cntrparam levels discrete %s", il_str));
### "дискретные уровни cntparam в gset %s"
gset parametric;
### [7] Отрисовка
gsplot z_splot;
### [8] Переключение в режим PostScript и отрисовка в файл
gset terminal push;
gset terminal postscript;
gset output "oct3.eps";
replot;
gset terminal pop;
gset output;
gset noparametric;
После проработки примеров с двухмерным графиком дискретных функций и графиком трехмерной функции, первые три блока [1-3] не должны вызвать много вопросов. В блоке [4], однако, я был вынужден прибегнуть к "фокусу", который покажет себя в блоке [6]. Хитрость в том, чтобы изобразить изолинии с помощью функции, определяемой пользователем. Значения этой функции и, следовательно, положение изолиний, не известны заранее.
В Gnuplot предлагается несколько способов определения изолиний, например
автоматическое вычисление заданного числа (линейно распределенных)
контуров или задание минимального и максимального значения приращения
между двумя соседними контурами. Наша задача требует более общего
решения, поскольку изолинии неравномерно распределены по оси z.
Для изолиний с полностью произвольными значениями, Gnuplot предлагает
третий способ, с помощью команды gset:
gset cntrparam discrete z1, z2, ..., zN
где z1, z2, ..., zN педставляют величины z-ой изолинии, заданные как числа с плавающей точкой. Таким образом,
gset cntrparam discrete 0.2, 0.4, 0.8
является абсолютно правильным вызовом, в то время как
z1 = 0.2
z2 = 0.4
z3 = 0.8
gset cntrparam discrete z1, z2, z3
не приведет ни к чему, кроме вывода сообщения о синтаксической ошибке
gset cntrparam discrete iso_levels
Запомните, gset нужны литералы с плавающей точкой!
Мы оказываемся в тупике, из которого нас может вывести лишь применение "малой магии". Если мы предложим Octave полную строку вызова gset, такую, в которую "интерполированы" значения вектора iso_levels (программисты на Perl дни на пролет заняты именно этим), то дело оказывается "в шляпе". Вот как делается это фокус:
# Преобразуем массив iso_levels в строку разделенных запятыми значений.
# Octave использует спецификатор формата повторно, если имеется больше
# значений для вывода, чем спецификаторов преобразвания формата.
# Не советую пробовать этот фокус с pritf из С :-)
il_string = sprintf("%f,", iso_levels)
# Удалим запятую после последнего значения в строке.
il_string = il_string(1 : length(il_string)-1)
# Применяем трюк с интерполяцией во второй раз
gset_string = sprintf("gset cntrparam levels discrete %s", il_string);
# Выполняем команду, сохраненную в переменной gset_string
eval(gset_string);
Для читетелей, не любящих абстрактные описания, привожу протокол выполнения (длинные строки были отредактированы для того, чтобы "вписаться" по ширине):
octave:10> il_string = sprintf("%f,", iso_levels)
il_string = 0.583444,0.592029,0.652120,0.815224,1.132847,1.656497, \
2.437679,3.527900,4.978667,6.841486,9.167864,12.009307,
octave:11> il_string = il_string(1 : length(il_string)-1)
il_string = 0.583444,0.592029,0.652120,0.815224,1.132847,1.656497, \
2.437679,3.527900,4.978667,6.841486,9.167864,12.009307
octave:12> gset_string = sprintf("gset cntrparam levels discrete %s", \
il_string)
gset_string = gset cntrparam levels discrete 0.583444,0.592029, \
0.652120,0.815224,1.132847,1.656497,2.437679,3.527900, \
4.978667,6.841486,9.167864,12.009307
В этом скрипте не вводится временная переменная gset_string, вместо этого sprintf() посылает свой вывод напрямую eval().
Блок [6]: Gnuplot не блещет в отрисовке контуров. На самом деле
руководство по GNUPlot предлагает не использовать эту функцию напрямую.
Мы, тем не менее, продолжим, поскольу наш подход легче для понимания.
Три следующих вызова gset переключает Gnuplot в режим
рисования контуров:
gset contour base # draw contours in the xy-plane
gset nosurface # do not draw the surface's mesh
gset view 0, 0 # view the xy-plane from above
Блоки [7] и [8] очень похожи на те, которые мы уже видели в разделах Octave: двухмерный график дискретных данных и Octave: Трехмерный график функции.
Дополнительные примеры графиков для Gnuplot можно найти на странице http://www.gnuplot.org/gnuplot/gpdocs/all2.htm
Scilab
А теперь поговорим о совершенно другом подходе...
Преодолевая проблему сложности, которую мы обсуждали в
разделе о всеобъемлющей сложности, Scilab [читается Сай-лэб] идет
другим путем (не таким путем надо было идти -- прим. пер.:)))).
В противоположность Gnuplot, Scilab не проводит строгого разделения
между отрисовкой и конфигурированием [графической подсистемы], предлагая
вместо этого (запустите scilab, а потом попробуйте команду apropos
plot) обилие различных "рисовательных" команд, создающих
графики разных видов. Более того, сами функции рисования [plot functions]
принимают множество параметров, меняющих внешний вид графиков. Некоторые
из этих аргументов выглядят прямо как шифровки, так что вы наверняка
захотите иметь под рукой соответствующие страницы руководства.
Для тех, кто хотел бы взглянуть онлайновую справку, не устанавливая Scilab, руководство можно скачать из Сети.
Scilab: двухмерный график дискретных данных
// Как всегда, для предотвращения проблем с кириллицей,
// аргументы функций не переводятся, а поясняются в комментариях.
// [1] Считать наборы данных set_i в N_i-Х-2 матрицы
set1 = read("l1.ascii", -1, 2);
set2 = read("l2.ascii", -1, 2);
set3 = read("l3.ascii", -1, 2);
// [2] Очистка графического окна
xbasc();
// [3] Нарисовать график; 1-я команда рисования определяет внешний вид графика
plot2d(set1(:, 1), set1(:, 2), -1, "011", ...
rect = [0, 8e-8, 100, 2e-6]);
plot2d(set2(:, 1), set2(:, 2), -2, "000");
plot2d(set3(:, 1), set3(:, 2), -3, "000");
// [4] Зададим оформление
xtitle(["Comparison of sets", "L1, L2, and L3"], ...
"Temperature / K", "Voltage / V");
// "Сравниваем наборы L1, L2 и L3", "Температура/K", "Напряжение/V"
legends(["Set L1 ", "Set L2 ", "Set L3 "], [-1, -2, -3], 2);
// "Набор L2 ", и т.д. Справедливости ради следует заметить,
// что в моей версии Scilab'а (2.4.5.что-то) из ALTLinux Spring 2001
// функции legends не оказалось ни в программе, ни в справке:(
// но она точно появилась в версии 2.6, так что следите и обновляйтесь
// дело того стоит. -- прим. переводчика
// [5] Сохраняем содержимое окна с графиком в файл, преобразовав его в PostScript
xbasimp(0, "sci1.xps");
unix("scilab -save_p sci1.xps.0 Postscript");
![[Рисунок: смотрите заголовок к разделу Octave: двумерный график
дискретных данных.]](misc/spiel/sci10000.png)
Здоровенный файл в Encapsulated Postscript
можно скачать (при желании).
Блок [1] считывает данные из файлов в матрицы.
Блок [2] очищает графическое окно (если оно уже есть). Важнее то, что xbasc() стирает все записанные в в окно графические команды. xbasc() расшифровывается, как [x-bas-c]: функции для работы с x11, базовый уровень, очистка [clear].
Намек: развлекаясь с функциями рисования графиков Scilab, очистка окна перед вызовом функций отрисовки часто экономит нажатие на клавиши: команда
xbasc(); plot2d(...);
написанная в одну строку может быть легко "возвращена" в для редактирования и вновь вызвана одним нажатием на клавишу return.
А вот в блоке [3] тайное письмо появляется во всей своей красе! Что, в самом деле, означает следующая конструкция?
plot2d(set1(:, 1), // вектор абсцисс
set1(:, 2), // вектор ординат
-1, // индеск стиля
"011", // управление оформлением
rect = [0, 8e-8, 100, 2e-6]); // размер графика
Я добавил комментарии для каждого аргумента, но к чему относится "индекс стиля" со значением -1? К скверно одетому хакеру? И что означают строка "управления оформлением"?
- Индекс стиля [style index]
- устанавливает внешний вид маркеров, изображающих значения данных или цвет линий, которые эти точки соединяют. Положительное значение i означает: рисовать линию цветом i, отрицаетльное: используй маркер вида abs(i). Обратите внимание на то, что plot2d() изображает либо линии, либо маркеры, но не и то, и другое. Если для одного и того же набора данных нужны и маркеры, и линии, то потребуются две отрисовки графика с разными индесами стиля.
- Управление оформлением
[decoration control]
- всегда строка длинной 3. Каждая буква управляет определенным аспектом
внешнего вида графика.
- Первый символ
- Включает/выключает вывод заголовка графика. Ноль '
0' означает отсутствие заголовка, а единица '1' дает Scilab'у команду изобразить заголовок. - Второй символ
- Упавляет тем, как вычисляется размер графика. Допустимые значения
от '
0' до '8'. За подробностями обращайтесь к документации по plot2d().В нашем примере мы используем '
1' для первой кривой и '0' для остальных. '1' позволяет пользователю явно указать plot2d() необходимость получить диапазон значений графика из аргументаrect. Если plot2d() вызван с '0', то используется размер уже имеющегося графика, без проведения каких-либо вычислений. - Третий символ
- Устанавливает тип осей. Можно выбрать из шести разных значений.
Мы выбрали '
1' для первой кривой, что создает оси внизу и по левому краю графика. Следующие кривый выводятся со значением '0', что подавляет отрисовку осей.
- Первый символ
Уф, немалый кусок отхватили! Блок [4] дает нам возможность отдохнуть.
xtitle([title_line1; title_line2; ...], x_label, y_label)
Добавляет к существующему графику заголовок (возможно из нескольких строк) и при необходимости украшает оси x и y текстовыми обозначениями.
legends([legend_1, legend_2, ...], [style_1, style_2, ...], position)
Помещает на график легенду в соответствии с указаниями, получаемыми в параметре position. Значение position = 1 указывает на "северо-восточный" угол. Остальные углы нумеруются по часовой стрелке, так что position = 2 поместит легенду в "северо-западный" угол. Параметры style_i имеют тот же смысл. что и числа, которые мы использовали в индексе стиля при вызове plot2d(). Они определяют то, какой тип маркетов или линий рисуется справа от текста легенды. Сам текст указывается в legend_i.
И наконец блок [5] преобразует данные графического окна в Postscript-файл. Команда
xbasimp(0, "sci1.xps")
заново проигрывает все графические команды для окна с номером 0 (а это как раз наше единственное графическое окно) в файл sci1.xps. Название функции не имеет ничего общего с демоном X11 по имени "bas"', а происходит от x11 и basic, как в случае xbasc(). Окончание "imp" происходит от французского "imprimer", что означает "печать". Из какого языка к нам пришло название "fsck"? Думаю, из языка N vcls.
Файл sci1.xps содержит почти правильный Postscript, но не совсем. Его содержимое должно быть обработано командой Scilab
scilab -save_p sci1.xps.0 Postscript
которая добавляет правильный заголовок Postscript и перемещает график на странице. "Внешний" Scilab вызывается функцией unix("комманды шелла").
Scilab: трехмерный график функции
// [1] Определим функцию
function z = f(u, v)
// ограниченная [truncated] функция Rosenbrock'а
z = 100.0*(v - u.^2).^2 + (1.0 - u).^2
z(find(z > 100)) = 100;
endfunction
// [2] Зададим сетку для вычисления f()
x = linspace(-3, 3, 40);
y = linspace(-2, 4, 40);
// [3] Очистим содержимое графического окна
xbasc();
// [4] Отрисовка
fplot3d(x, y, f, 65, 1.5);
// [5] Займемся украшательсвом
xtitle("Rosenbrock Function", "u", "v");
// [6] Сохраним содержимое окна в файле; преобразуем в PostScript
xbasimp(0, "sci2.xps");
unix("scilab -save_p sci2.xps.0 Postscript; " ..
+ "gzip --best --force sci2.eps");
А здесь сжатая версия в формате Encapsulated Postscript.
После обилия нового материала в разделе Scilab: двухмерный график дискретных данных в этом разделе все новости прячутся в блоке [4]:
fplot3d(x_vector, y_vector, function_of_x_and_y, alpha, theta)
Векторы x_vector и y_vector определяют "сетку", на которой вычисляется функция function_of_x_and_y. Сравнивая fplot3d() с gsplot из Octave, можно заметить, что Scilab создает "решетку" [grid] за нас. fplot3d() -- это надстройка, созданная для удобства над
plot3d(x_vector, y_vector, z_matrix, alpha, theta)
которая, в свою очередь, уже напоминает gsplot (и mesh() из Tela).
Параметры theta и alpha задают высоту и поворот (относительно оси z) камеры [view point] (Чертежники, возможно, знают другое название для view point, но в трехмерке это обычно называется "камера" (в смысле -- видеокамера) -- прим. пер.).
Scilab: контурный график функции
// [1] Определим функцию
function z = g(u, v)
z = exp(u) .* (4.0*u.^2 + 2.0*v.^2 + 4.0*u.*v + 2.0*v + 1.0)
endfunction
// [2] Определим весовую функцию для расстояния между изолиниями
function y = pow_weight(x, n)
// Отобразим интервал в себя и "взвесим", возводя в степень.
d = max(x) - min(x)
y = d*((x - min(x))/d).^n + min(x)
endfunction
// [3] Зададим "решетку" для вычисления g()
x = linspace(-4.5, -0.5, 40);
y = linspace(-1.0, 3.0, 40);
// [4] Вычислим g() на точках, заданных X и Y
z = eval3d(g, x, y);
// [5] Рассчитаем расстояния изолиний
iso_levels = pow_weight(linspace(min(z)*1.01, max(z)*0.99, 12), 3.0);
// [6] Очистим графическое окно
xbasc();
// [7] Установим формат для изолиний, аннотаций и графика
xset("fpf", "%.2f");
contour2d(x, y, z, iso_levels);
// [8] Украшения для "Контурного графика g(u, v)"
xtitle("Contour Plot of g(u, v)", "u", "v");
// [9] Сохраним графическое окно в файл; преобразуем в PostScript
xbasimp(0, "sci3.xps");
unix("scilab -save_p sci3.xps.0 Postscript");
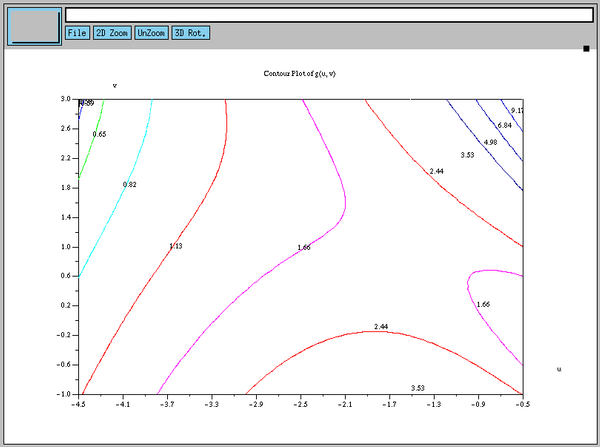
Можно взять результат в готовом для печати виде (eps).
Помните трудности, которые мы испытывали, задавая определяемые пользователем изолинии в Octave/Gnuplot? В Scilab проблема решается без фокусов, магии или взяток. Так же, как в случае plot3d(), Scilab определяет вспомогательную [convenience] функцию
fcontour2d(x_vector, y_vector, function_of_x_and_y, levels)
служащую "оберткой" для
contour2d(x_vector, y_vector, z_matrix, levels)
Но, поскольку нам необходимо знать максимальное и минимальное значение, принимаемое g(u, v) на "решетке", fcontour2d() ни в чем не облегчит нашей задачи. Так что в блоке [4] мы вычисляем g(u, v) на точках "сети", задаваемой векторами x и y:
z = eval3d(g, x, y)
В блоке [7] мы используем z и iso_levels из
блока [5]. Вызов xset() использует формат вывода числе
с плавающей запятой [floating point
format] ("fpf") в "%.2f",
спецификатор формата C-printf, который гарантирует, что все числа
на контурных линиях будут иметь две цифры после запятой.
Остальные блоки используют уже известные функции.
На посвященном Scilab сайте INRIA можно найти дополнительные демонстрации возможностей построения графиков.
Помимо проиллюстрированных выше функций, Scilab предовтавляет много возможностей. Например:
- Низкоуровневые функции для отрисовки точек, линий, многоугольников и т.д.
- Участки поверхностей [surface facets], которые могут служить строительными блоками для трехмерных конструкций. (Взгляните на удивительные примеры, созданные Энрико Сержем [Enrico Segre] на Scigallery)
- Высокоуровневые фунции создания пользовательского интерфейса для быстрой разработки "пошитых на заказ" приложений Scilab.
- Функции обратной связи, позволяющие передовать в программу информацию из любого графического окна Scilab.
Tela
В разделах об Octave и Scilab
мы видели, что обе программы сохраняют вспомогательное "состояние"
окна отрисовки графика. В максимальной степени это делает Gnuplot:
вызовы gplot или gsplot практически не
принимают параметров. Состояние управляется командами gset.
Scilab сохраняет лишь некоторую часть состояния графического окна,
примером могут служить легенда и заголовок.
В Tela для создания графиков используется дополнительное приложение
PlotMTV. И PlotMTV, и Tela находятся на противоположном конце спектра:
графические окна не имеют сохраняемого состояния и все фактические
параметры создаваемого графика должны быть указаны прямо в вызове
фунции отрисовки. Преимуществом использованного в Tela подхода является
то, что несколько одновременно создаваемых графиков не мешают друг
другу (как мы скоро увидим, это происходит до тех пор, пока мы их
не заставим с помощью вызовов hold(on) и hold(off)).
"Длиннота" вызова функций отрисовки графиков -- отрицательная
сторона такого подхода.
Как и при обсуждении других программ рисования, руководство по PlotMTV полезно иметь под рукой.
Tela: двумерный график дискретных данных
// [1] Считаем i-й набор данных в матрицу N_i на 2
set1 = import1("l1.ascii");
set2 = import1("l2.ascii");
set3 = import1("l3.ascii");
// [2] Определение функции отрисовки графиков
function do_plot(d1, d2, d3)
{
hold(on); // задержим фактическую отрисовку до вызова hold(off)
// отрисовка 1-го набора данных
plot(d1[:, 1], d1[:, 2],
"linestyle", 0,
"markertype", 2,
"linelabel", "Набор данных L1",
// Займемся украшениями
"toplabel", "Сравнение наборов данных",
"subtitle", "L1, L2, и L3",
"xlabel", "Температура / K",
"ylabel", "Напряжение / V",
// Определим область отрисовки
"xmin", 0,
"xmax", 100,
"ymin", 8e-8,
"ymax", 2e-6);
// отрисовка 2-го набора данных
plot(d2[:, 1], d2[:, 2],
"linestyle", 0,
"markertype", 3,
"linelabel", "Набор данных L2");
// отрисовка 3-его набора данных
plot(d3[:, 1], d3[:, 2],
"linestyle", 0,
"markertype", 4,
"linelabel", "Набор данных L3");
hold(off); // plot!
};
// [3] Отрисовка в окно X11
do_plot(set1, set2, set3);
// [4] Отрисовка в файл postscript
plotopt("-o tela1.eps -printcmd 'cat' -noxplot -print");
do_plot(set1, set2, set3);
Мда, этот скрипт не похож на предыдущие! Именно так -- мне пришлось прибегнуть к новому приему для того, чтобы избежать проблем с отсутствием сохраняемых состояний в функциях отрисовки. Поскольку Tela "забывает" о параметрах после отображения графика в окне X11, для перенаправления вывода в файл Postscript мне пришлось бы "набивать" все по новой. Ну, а дублирование кода -- корень многих (но не всех:) зол. Поэтому пришлось "завернуть" отрисовку графиков в Tela в отдельную функцию. Дальше мы получаем изображение графика в окне X11, а затем, изменив выходной файл и его тип, снова выполним отрисовку, но уже в файл eps:
do_plot(...); // вывод в окно X11
plotopt("-o foo.eps -printcmd 'cat' -noxplot -print");
// перенаправление вывода
do_plot(...);
// выполняем отрисовку в формате Encapsulated Postscript
// в файл foo.eps
![[Graphics: Please see the image caption of '2D Discrete Data Plot' in the Octave section.]](misc/spiel/tela1000.png)
Версия графика в формате Encapsulated
Postscript.
Функция do_plot в блоке [2] берет на себя заботу об использовании функции plot(). Общая структура вызова plot(), а на самом деле всех функций для отрисовки графиков в Tela, такова: сначала передаем обязательные агрументы с "датосодержащими" векторами или матрицами, а затем помеченные ключами [key-value pairs] необязательные строки.
plot(x_vector, y_vector // данные
"option_key1", "option_value1", // 1-я опция
"option_key2", "option_value2", // 2-я опция
...
"option_keyN", "option_valueN"); // N-я опция
Обратите внимания на то, что написание каждой пары ключ-значение в отдельной строке повышает читаемость вызова в целом.
Строковые пары ключ-значение понятны сами по себе. Не вполне очевидные соответсвия вроде linestyle => 0 (= невидимой линии) или markertype => 2 (= крестики) необходимо предварительно найти в руководстве или в в примерах по созданию графиков, которые демонстрируют все доступные стили.
Tela: трехмерный график функции
function v = linspace(a, b; n)
{
if (isdefined(n)) nn = n else nn = 100;
v = a + (0 : nn - 1) * (b - a) / (nn - 1)
};
// [1] определение функции
function z = f(u, v)
{
// ограниченная [truncated] функция Rosenbrock'а
z = 100.0*(v - u^2)^2 + (1.0 - u)^2;
z[find(z > 100.0)] = 100.0;
};
// [2] Вычисляем f() на заданных точках
x = linspace(-3.0, 3.0, 40);
y = linspace(-2.0, 4.0, 40);
[xx, yy] = grid(x, y);
zz = f(xx, yy);
// [3] определение функции рисования
function do_plot(x, y, zz)
{
mesh(zz,
"xgrid", x,
"ygrid", y,
"toplabel", "Rosenbrock Function",
"xlabel", "u",
"ylabel", "v",
"hiddenline", "true",
"eyepos.z", 2.0)
};
// [4] отрисовка в окно X11
do_plot(x, y, zz);
// [5] отрисовка в файл postscript
plotopt("-o tela2.eps -printcmd 'cat' -noxplot -print");
do_plot(x, y, zz);
system("gzip --best --force tela2.eps");
![[Graphics: Please see the image caption of '3D Function Plot' in the Octave section.]](misc/spiel/tela2000.png) "Зазипованная" версия
файла Encapsulated Postscript (eps.gz) тоже имеется.
"Зазипованная" версия
файла Encapsulated Postscript (eps.gz) тоже имеется.
В Tela нет встроенной функции linspace(), так что ее мне пришлось написать на скорую руку.
Блок напоминает блок [2] в разделе Octave: трехмерный график функции, где meshgrid() из Octave заменен на grid() из Tela.
Функция mesh(), рисующая трехмерный график, в качестве первого аргумента принимает матрицу z-значений, а спецификация "решетки" указывается в опциях:
mesh(z_matrix,
"xgrid", x_vector,
"ygrid", y_vector);
Понятно, что размерности z_matrix, x_vector y_vector и должны быть согласованы.
Tela: Контурный график функции
function v = linspace(a, b; n)
{
if (isdefined(n)) nn = n else nn = 100;
v = a + (0 : nn - 1) * (b - a) / (nn - 1)
};
// [1] определение функции
function z = g(u, v)
{
z = exp(u) * (4.0*u^2 + 2.0*v^2 + 4.0*u*v + 2.0*v + 1.0)
};
// [2] весовые функции для определения расстояний
// между излолиниями
function y = pow_weight(x, n)
{
// Map interval X onto itself, weight with N-th power.
d = max(x) - min(x);
y = d*((x - min(x))/d)^n + min(x)
};
// [3] Вычисляем f() в заданных точках
x = linspace(-4.5, -0.5, 40);
y = linspace(-1.0, 3.0, 40);
[xx, yy] = grid(x, y);
zz = g(xx, yy);
// [4] Вычисляем расстояния между изолиниями
iso_levels = pow_weight(linspace(min(zz)*1.01, max(zz)*0.99, 12), 3.0);
il_str = sformat("``", iso_levels);
il_str = il_str[2 : length(il_str)];
// [5] Определение функции, рисующией график
function do_plot(x, y, zz, iso_levels_str)
{
contour(zz,
"xgrid", x,
"ygrid", y,
"toplabel", "Контурный график g(u, v)",
"xlabel", "u",
"ylabel", "v",
"contours", iso_levels_str)
};
// [6] Отрисовка в окне X11
do_plot(x, y, zz, il_str);
// [7] Отрисовка в postscript
plotopt("-o tela3.eps -printcmd 'cat' -noxplot -print");
do_plot(x, y, zz, il_str);
![[Graphics: Please see the image caption of 'Contour Function Plot' in the Octave section for the image's description.]](misc/spiel/tela3000.png)
Имеется и версия в Encapsulated Postscript, пригодная
для качественной печати.
В Tela по отношению к PlotMTV приходится прибегать к тому же трюку, который мы использовали, убеждая Octave передать в Gnuplot значения уровдней для контуров. Однако трюк, используемый в блоке [4], не столь хитер. Как и раньше, на первом шаге мы вычисляем вектор с изо-уровнями. Функция sformat() работает аналогично функции sprintf() в Octave, хотя формат векторов различен, что видно из протокола выполнения (il_str отредактирован для того, чтобы уместиться в строке):
>il_str = sformat("``", iso_levels);
>il_str
"#(0.583444, 0.592029, 0.65212, 0.815224, 1.13285, 1.6565, \
2.43768, 3.5279, 4.97867, 6.84149, 9.16786, 12.0093)"
PlotMTV понимает вектора, заключенные в скобки, но символ "решетки" нужно убрать
il_str = il_str[2 : length(il_str)];
il_string может быть передана в функцию contour(),
как значения именованного параметра contours.
Дополнительные демонстрационные графики, созданные с помощью PlotMTV можно найти на ORNL и на HSC (у меня что-то не вышло сходить по этим ссылкам:( -- прим. пер.).
Между прочим, PlotMTV прекрасно подходит на роль графического сервера [backend] для скриптов и программ "домашнего розлива". Руководство по PlotMTV неизменно помогает читателю в создании программных интерфейсов к собственным функциям.
Заключительные комментарии по графикам
Мы узнали о том, как в Octave, Scilab и Tela получить графики функций или экспериментальных данных, готовые для отправки в редакцию. Иногда, из-за ограничений реализации, потребовались довольно хитроумные приемы. Нам, однако, удалось разрешить все проблемы.
Мне кажется, что объем ручной работы, необходимой для создания действительно красивых графиков, всегда будет большим, вне зависимости от используемого программного обеспечения.
Кристоф Шпиль [Christoph Spiel]
Крис управляет консалтинговой компанией по открытому программному обеспечению в верхней Баварии, Германия. По своей специальности - физике -- у него есть докторская степень от Munich University of Technology -- его основные интересы лежат в области теории чисел, гетерогенных программных сред и программного инжиниринга. С ним можно связаться по адресу [email protected].
Copyright (C) 2001, Christoph Spiel.
Copying license http://www.linuxgazette.com/copying.html
Published in Issue 71 of Linux Gazette, October 2001
Вернуться на главную страницу
![[Рисунок: окно Gnuplot показывает 12 изолиний, каждую своим цветом.
График изображает седловую точку функции g(u, v) в своей правой трети.]](misc/spiel/oct30000.png)